ÜÇGENDE AÇIORTAY BAĞINTILARI
1. Açıortay
Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir.
Aşağıdakii şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir.
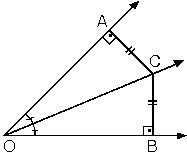
Açıortay üzerindeki herhangi bir noktadan açının kenarlarına çizilen dik uzunluklar eşittir.AOB bir açı,[OC açıortaym(AOC) = m(COB)
(AC)=(CB)
AOC ve BOC eşüçgenler olduğundan |OA| = |OB|
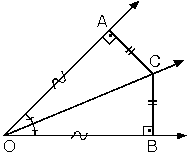
2. İç Açıortay Bağıntısı
ABC üçgeninde [AN] açıortay ABN ve ANC üçgenlerinin [BC] tabanına göre, yükseklikleri eşit olduğundan
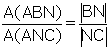 olur …..(1)
olur …..(1)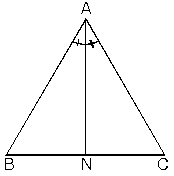
ABN üçgeninde [AB] kenarına ait yükseklik ANC üçgeninde [AC] kenarına ait yüksekliğe eşittir.
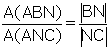 olur …..(2)
olur …..(2)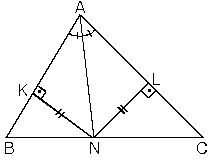
[AN] açıortay olmak şartıyla bu iki alan oranını birleştirirsek; (1) ve (2) den
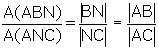 olur.
olur.
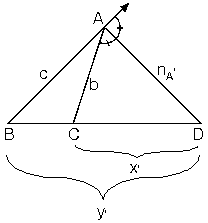
ABC üçgeninde [AN] açıortay olmak şartıyla 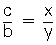
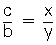
Buradan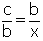 ve b.y=c.x eşitlikleri de elde edilir.
ve b.y=c.x eşitlikleri de elde edilir.
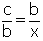 ve b.y=c.x eşitlikleri de elde edilir.
ve b.y=c.x eşitlikleri de elde edilir.3. İç Açıortay Uzunluğu
ABC üçgeninde A köşesinden çizdiğimiz açıortayuzunluğuna nA dersek 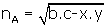
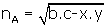
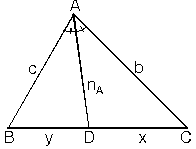
4. Dış Açıortay Bağıntısı
ABC üçgeninde [AD], A köşesine ait dış açıortaydır.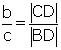
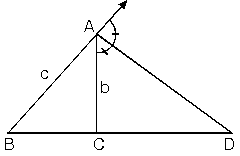
5. Dış Açıortay Uzunluğu
ABC üçgeninde [AD] dış açıortayının uzunluğunan’A dersek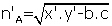
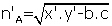
6. İç açıortayla dış açıortay arasındaki açı
m(DAE)=90°
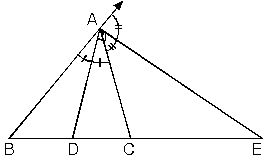
ABC üçgeninde [AD] iç açıortayı ile [AE] dış açıortayı arasındaki açı için
2a + 2b = 180°a + b = 90° dir.
[DA] ^[AE]
|
- Bir üçgende iç açıortayların kesim noktası iç teğet çemberin merkezidir.
P noktasının kenarlara uzaklığı eşittir. Merkezden indirilen dikmeler iç teğet çemberin yarıçapı olur.

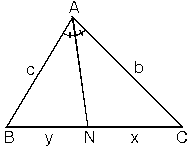
iç açıortay bagıntısı 3.şekilde orantıda yanlışlık var
YanıtlaSil